Table of contents

• What is Deformable Generator?

• Experimental results

What is Deformable Generator?

The deformable generator model is a deep generative model which disentangles the appearance and geometric information for both image and video data in purely unsupervised manner. The attributes of the visual data can be summarized as appearance (mainly including color, illumination, identity or category) and geometry (mainly including viewing angle and shape).

The deformable generator model contains two generators, the appearance generator network models the appearance related information, while the geometric generator network produces the deformable fields (displacement of the coordinate of each pixel). The two generator networks are combined by the geometric related warping, such as rotation and stretching, to obtain the final image or video sequences.

Two generators act upon independent latent factors to extract disentangled appearance and geometric information from image or video sequences (The nonlinear transition model is introduced to both the appearance and geometric generators to capture to dynamic information for the spatial-temporal process in the video sequences).

The deformable generator model finds its root in the Active Appearance Models (AAM) which separately learn the appearance and geometric information. Particularly, AAM utilizes linear model, i.e. principal component analysis (PCA), for jointly capturing the appearance and shape variation in an image. Unlike the AAM method which requires hand-annotated facial landmarks to model the shape for each training image, the deformable generator model is purely unsupervised and learns from images or videos alone.

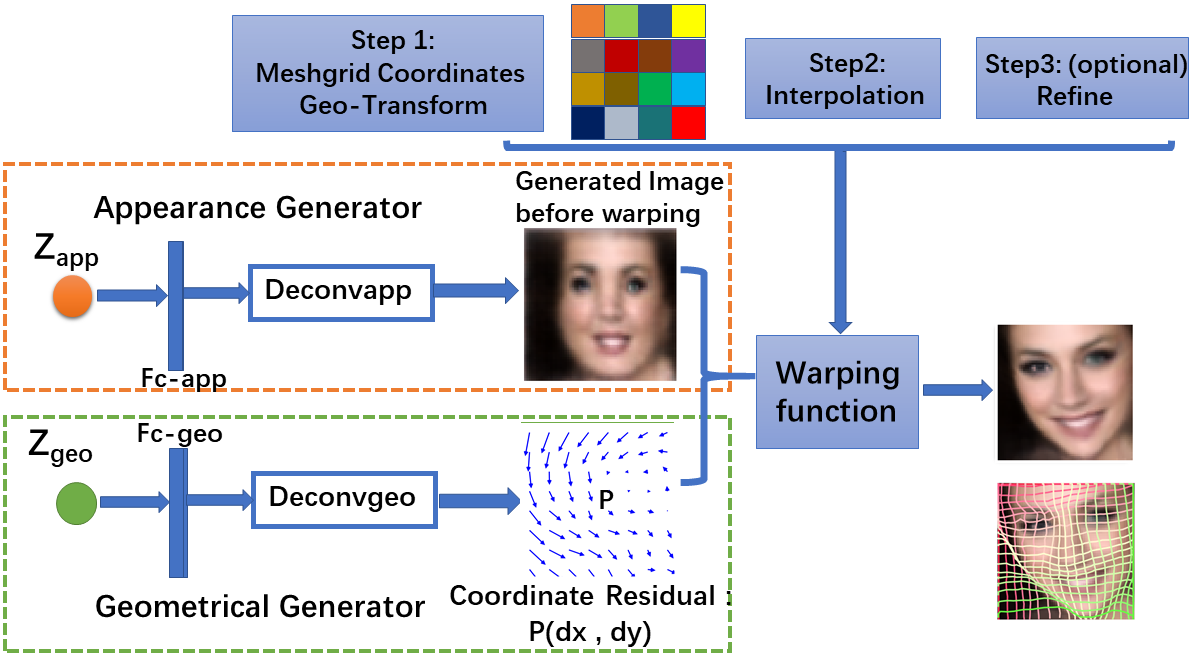
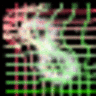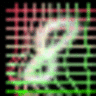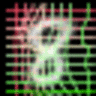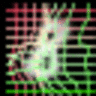
As we can observed, the canonical faces (generated image before warping) in the front view are auto-learned and produced by the appearance generator. By warping the output of the appearance generator with the deformable fields (coordinate residual \(P(dx,dy)\)) generated by the geometric generator, we obtain the final reconstructing images.

The model can be expressed as

where $Z^a \sim {\rm N}(0, I_{d_a})$, $Z^g \sim {\rm N}(0, I_{d_g})$, and $\epsilon \sim {\rm N}(0, \sigma^2 I_D)$ ($D = D_x \times D_y \times 3$) are independent. $F_w$ is the warping function, which uses the displacements generated by the geometric generator $F_g(Z^g;\theta_g)$ to warp the image generated by the appearance generator $F_a(Z^a;\theta_a)$ to synthesize the final output image $X$.

Experimental results

Experiment 1: Learn the disentangled basis functions for appearance and geometry

To study the performance of the proposed method in disentangling the appearance and geometric information, we first investigate the appearance basis functions and the geometric basis functions of the learned model. We train the deformable generator on the 10,000 random selected face images from CelebA dataset.

Typical appearance basis functions	Visualized by the generated images from interpolating the appearance latent factors along the basis functions.

Representive geometric basis functions	visualized by the generated images from interpolating the geometric latent factors along the basis functions

The appearance and the geometric latent factors can be interpreted as the projection or reconstruction coefficients along the direction of the corresponding appearance and geometric basis functions. Each dimension of the appearance latent factors encodes appearance information such as color, illumination and gender. Each dimension of the geometric latent factors encodes fundamental geometric information such as shape and viewing angle.

Rotation warping to the apearance basis functions	Shape warping to the apearance basis functions

we can apply the geometric warping (e.g. geometric basis functions in the figure) learned by the geometric generator to all the canonical faces (e.g. appearance basis functions in the figure) learned by the appearance generator.

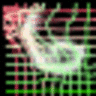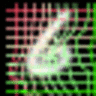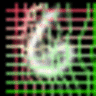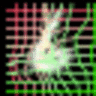
Experiment 2: Unsupervised landmark localization

Unsupervised landmark localization. Row 1: the samples of the testing images from the MAFL dataset. Row 2: the deformation grid estimated from warping the the canonical grid with the coordinate displacement (deformation fields) learned from the geometric generator. Row 3: the canonical grid overlapped on the canonical faces learned from the appearance generator. Row 4: the semantic landmark locations. The green points denote the ground truth, and the red points denote the predictions.

Experiment 3: Learn to transfer the appearance and geometric knowledge

Transferring and recombining geometric and appearance vectors	Transferring the learned expression from the gray dataset to the face images in the color Multi-PIE dataset.

Transferring and recombining geometric and appearance vectors. The first row shows 7 unseen faces from CelebA. The second row shows the generated faces by transferring and recombining 2th-7th faces’ geometric vectors with first face’s appearance vector in the first row. The third row shows the generated faces by transferring and recombining the 2th-7th faces’ appearance vectors with the first face’s geometric vector in the first row.

Experiment 4: Learn on non-face dataset

geometric interpolation results of cat and monkey faces after applying the rotation and shape warping learned from CelebA.	geometric interpolation results of the model learned from *car* category of CIFAR-10 dataset.

Geometric basis functions of viewing angles	Geometric basis functions of shapes.

On each row, we set $Z^a$ to be one of the discrete label, while interpolating one dimension of the geometric latent factor $Z^g$ from $[-\gamma,\gamma]$ with a uniform step $\frac{2\gamma}{10}$. The first column represent the images generated by the one-hot $Z^a$ (before warping by the deformable fields generated by $Z^g$), and the remain 10 columns show the results by interpolating the shape or the view factor of $Z^g$.

Experiments for Dynamically Deformable Generator

Experiment 5: Learn to transfer and combine the dynamical appearance and geometric knowledge

Transfer and recombine the appearance and geometric information from different video sequences.

Experiment 6: Dynamically Deformable fields for facial expression analysis and recognition

The facial expression is connected with the dynamically geometric information and unrelated with the appearance information, such as color, illumination, and identity. The learned dynamically deformable fields can be used for facial expression analysis and recognition.